Home| Scope |Types/Configs. |Schematics |Heat Balance |Heat Trans1 |Heat Trans2 |Process |Circulation |Other |Publications |Calculators
Process
Thermal properties of water and steam
Thermal properties of flue gas
Combustion, supplementary firing
Heat transfer coefficients
Intube pressure drop
Gas side pressure drop across tubes
Ducting pressure losses
Acid dew point of flue gas
NOx and other considerations

Thermal properties of water and steam

The properties of water and steam have been described by the “International Association for the Properties of Water and Steam”. The latest release is the IAPWS97 document, which is available at this site under publications. This document includes formulas for the various properties which make it fairly simple to develop software for use in HRSG design and rating. The formulation suggested for industrial use is the IAPWS-IF97 which replaces the 1967 document, IFC67. It should be noted that there is no significant differences in these two sets of formulations, in the pressure and temperature ranges normally used in HRSGs. The following JavaScript calculator is based on the IFC67 formulations. This calculator has not been tested throughout the overall range of pressure and temperatures covered by these formulations, but should be sufficient for the purposes of this introduction to HRSG design.


Thermal properties of flue gas

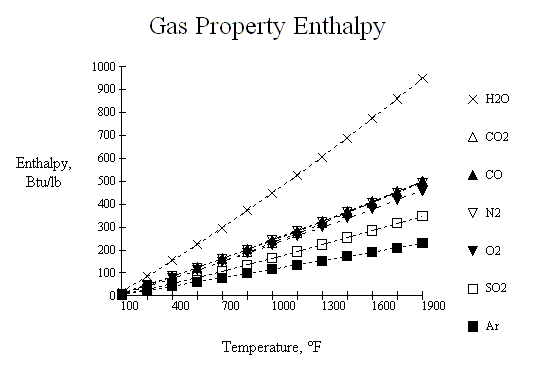
The thermal properties for flue gas used in these procedures are curve fits of the following families of curves. The source for these curves is not currently known, as they were originally constructed some thirty years ago as we were developing some of the software proceedures presented herein. However, the reliability of these values seem to be very suitable for HRSG design.

Flue Gas Enthalpy
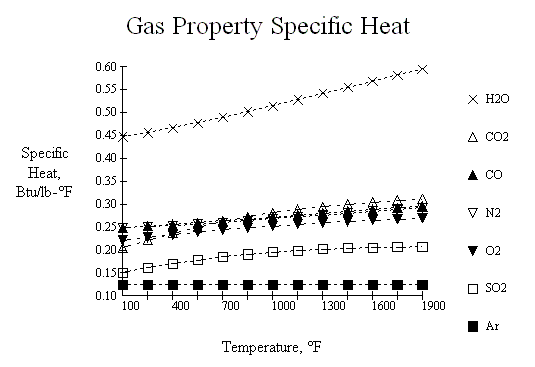
Flue Gas Specific Heat
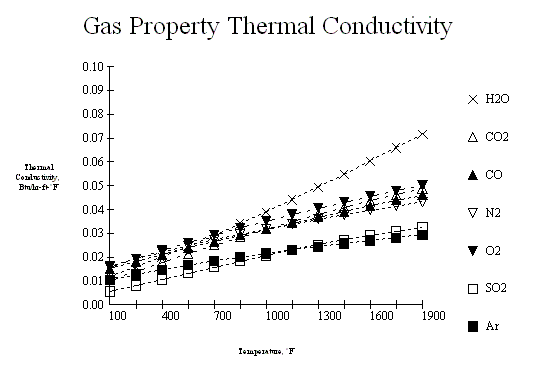
Flue Gas Thermal Conductivity
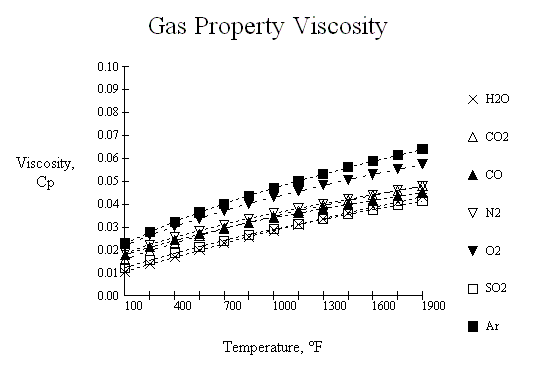
Flue Gas Viscosity
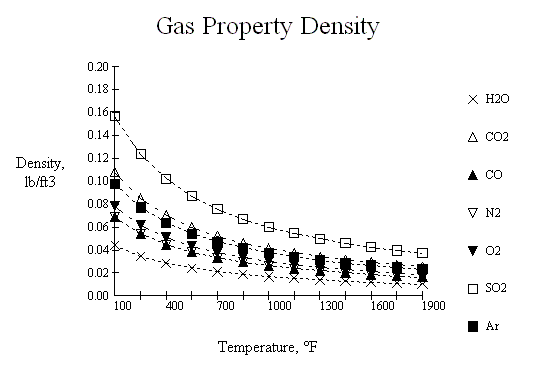
Flue Gas Density

Below is a JavaScript calculator which can interpret these curves.


Combustion, supplementary firing

The supplemental combustion in HRSG systems takes place in a burner which usually is located in the flue gas stream going to the HRSG. However, some systems because of high firing requirements and low O2 in the flue gas, may require to be fired externally to the flue gas stream and may reuire additional combustion air. The types of burners and how they function are not covered in detail in this section. The amount of heat released can be easily calculated for a gas when we know the composition of the fuel and the heating values of the various components. For liquid fuels, the heating values are obtained by a calorimeter test.
From these values and using the standard combustion equation, we can determine the composition of the flue gas leaving the burner. As an example, the combustion of methane could be stated :

CH4 + 2O2 --- > CO2 + 2H2O
Of course for fuel gases containing many more components and burning in flue gas rather than pure oxygen, the equation gets more complicated. Therefore, a task that in itself is quite simple, becomes a burden to do by hand, but can be easily accomplished by a simple computer program. The heating values normally used in HRSG design are the LHV, lower heating values.
To try some calculations, click the button below to open another window to do some fuel combustion calculations:


The following Lower Heating Values(LHV) are used in this script:
ComponentBtu/lb ComponentBtu/lb ComponentBtu/lb
CH421,520 C2H620,432 C3H819,944
N-C4H1019,680 I-C4H1019,629 N-C5H1219,517
I-C5H1219,478 C6H1419,403 CO4,347
H251,623 N20 CO20
C14,093 S3,983 C2H420,295
C3H619,691 C4H819,496 C6H617,480
H2O0 O20 H2S6,545

Heat Transfer Coefficients

The inside film coefficient needed for the thermal calculations may be estimated by several different methods. The API RP530, Appendix C provides the following methods,

For liquid flow with Re =>10,000,
hl = 0.023(k/di)Re0.8*Pr0.33(mb/mw)0.14
And for vapor flow with Re =>15,000,
hv = 0.021(k/di)Re0.8*Pr0.4(Tb/Tw)0.5
Where the Reynolds number is,
Re = di*G/mb
And the Prandtl number is,
Pr = Cp*mb/k
Where,
hl = Heat transfer coefficient, liquid phase, Btu/hr-ft2-°F
k = Thermal conductivity, Btu/hr-ft-°F
di = Inside diameter of tube, ft
mb = Absolute viscosity at bulk temperature, lb/ft-hr
mw = Absolute viscosity at wall temperature, lb/ft-hr
hv = Heat transfer coefficient, vapor phase, Btu/hr-ft2-°F
Tb = Bulk temperature of vapor, °R
Tw = Wall Temperature of vapor, °R
G = Mass flow of fluid, lb/hr-ft2
Cp = Heat capacity of fluid at bulk temperature, Btu/lb-°F
For two-phase flow,
htp = hlWl + hvWv
Where,
htp = Heat transfer coefficient, two-phase, Btu/hr-ft2-°F
Wl = Weight fraction of liquid
Wv = Weight fraction of vapor
The following script will allow us to try these formulas out using our browser.
Tube diameter, in: Mass flow, lb/hr-ft2:
Percent vapor, %: Bulk Temp., °F:
Liquid PropertiesVapor Properties
Thermal cond., Btu/hr-ft-°F: Thermal cond., Btu/hr-ft-°F:
Visc. bulk, lb/ft-hr: Visc. bulk, lb/ft-hr:
Spec. Heat, Btu/lb-°F: Spec. Heat, Btu/lb-°F:
Visc. @ wall, lb/ft-hr: Temp. @ wall, °F:


hl Coefficient, Btu/hr-ft2-°F:
hv Coefficient, Btu/hr-ft2-°F:
htp Coefficient, Btu/hr-ft2-°F:
Reynolds number:LiquidVapor
It should be stressed at this time, that there are many ways to calculate the inside heat transfer coefficient, and a lot of care should be taken in the procedure selected for use in HRSG design. Other methods, such as HTRI, Maxwell, Dittus-Boelzer, or others may be more appropriate for a particular HRSG design. You will notice that we have not offered a method for film boiling coefficient. The reason for this ommision is that in the evaporator, when the hi is high, which it is for the boiling case, it does not have any significant effect on the calcuations. We would recommend that a value of 1,500 to 2,000 Btu/hr-ft2-°F be used for these cases.
Intube Pressure Drop

The intube pressure drop may be calculated by any number of methods available today, but the following procedures should give sufficient results for HRSG design. The pressure loss in HRSG tubes and fittings is normally calculated by first converting the fittings to an equivalent length of pipe. Then the average properties for a segment of piping and fittings can be used to calculate a pressure drop per foot to apply to the overall equivalent length. This pressure drop per foot value can be improved by correcting it for inlet and outlet specific volumes.

Friction Loss:
Dp = 0.00517/di*G2*Vlm*F*Lequiv
Where,
Dp = Pressure drop, psi
di = Inside diameter of tube, in
G = Mass velocity of fluid, lb/sec-ft2
Vlm = Log mean specific volume correction
F = Fanning friction factor
Lequiv = Equivalent length of pipe run, ft
And,
Vlm = (V2-V1)/ln(V2/V1)
For single phase flow,
V1 = Specific volume at start of run, ft3/lb
V2 = Specific volume at end of run, ft3/lb
For mixed phase flow,
Vi = 10.73*(Tf/(Pv*MWv)*Vfrac+(1-Vfrac)/rl
Where,
Vi = Specific volume at point, ft3/lb
Tf = Fluid temperature, °R
Pv = Press. of fluid at point, psia
MWv = Molecular weight of vapor
Vfrac = Weight fraction of vapor %/100
rl = Density of liquid, lb/ft3
Fanning Friction Factor:
The Moody friction factor, for a non-laminar flow, may be calculated by using the Colebrook equation relating the friction factor to the Reynolds number and relative roughness. And the Fanning friction factor is 1/4 the Moody factor. For a clean pipe or tube, the relative roughness value for an inside diameter given in inches is normally 0.0018 inch.
With this, we can calculate the factor,
Reynolds number =
Inside Diameter, inches =
Friction factor, F:
Equivalent Length Of Return Bends:

The equivalent length of a return bend may be obtained from the following curves based on Maxwell table and can be corrected using the Reynolds number correction factor.

Lequiv = FactNre*Lrb
Where,
FactNre = Reynolds number correction
Lrb = Equivalent length of return bend, ft
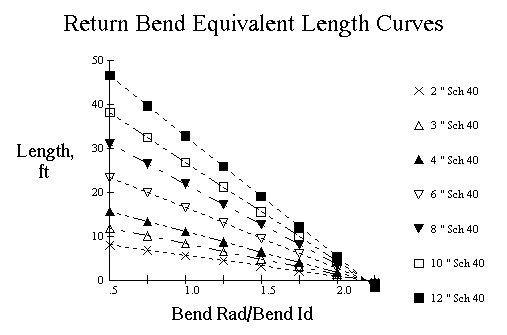
Return Bend Equivalent Length:
Return Bend Equivalent Length
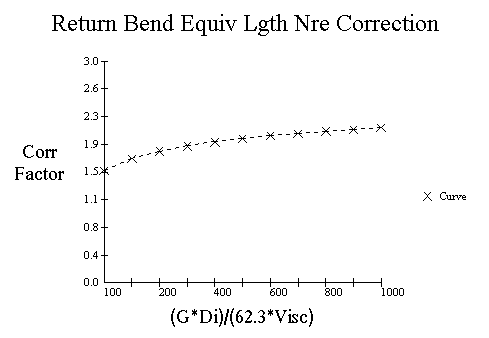
Reynolds Correction:
Reynolds Correction
Where,
G = Mass velocity, lb/sec-ft2
Di = Inside tube diameter, in
Visc = Viscosity, cp

Now that we have all the details described, we can calculate the pressure drop for some typical heater coils.

Coil Data
Tube inside dia., in: Pipe straight length, ft:
Bend radius, in: Number of returns:
Process Data
Mass vel., lb/sec-ft2: Viscosity, cp:
Spec. vol. at start, ft3/lb: Spec. vol. at end, ft3/lb:
Pressure Drop, psi: