
| Home | | | Scope | | | Types/Configs. | | | Schematics | | | Heat Balance | | | Heat Trans1 | | | Heat Trans2 | | | Process | | | Circulation | | | Other | | | Publications | | | Calculators |
In-direct, non-luminous radiation in an HRSG design is only significant to consider when the flue gases are above 1,000 °F. This normally would occur only following supplementary firing of the flue gas. It should be noted that there may also be some direct radiation occur in an HRSG if the duct burners are located directly in front of the HRSG heat transfer sections. For most designs, however, simply considering the radiation using the following method will suffice. If the HRSG is designed with an evaporator shield section, i. e., there is an evaporator coil placed between the burner and a superheater coil, there usually is no problem with tube wall temperature due to indirect, non-luminous, radiation. But if there is no shield coil, the superheater coil needs to be checked carefully to make sure that maximum tube wall temperature is not exceeded.
 | In an HRSG similar to this one, the superheater tubes are directly exposed to the hot gases and flame in the combustion chamber. They are also exposed to the heat radiated off the refractory lined combustion chamber in front of the tubes. To calculate the heat transfered to these tubes by radiation, we will use the methods described below. |
| qn = Non-luminous radiant heat transfer to the tubes, Btu/hr |
| s = Stefan-Boltzman constant, 0.173E-8 Btu/ft2-hr-R4 |
| a = Relative effectiveness factor of the tube bank |
| Acp = Cold plane area of the tube bank, ft2 |
| F = Exchange factor |
| Tg = Effective gas temperature in firebox, °R |
| Tw = Average tube wall temperature, °R |
For a single row in front of a refractory wall, use Total One Row. For two rows in front of a refractory wall, use Total Two Rows. For double sided firing, use Direct One Row.

Since all the radiant heat directed toward this bank of tubes is absorbed by the tubes in the convection, the relative absorption effectiveness factor, a, for the tubes can be taken to be equal to one.
Cold Plane Area, Acp :The cold plane area for the tube section is equal to the cold plane area of the first row of tubes.
Acp = Ntube*Stube*LtubeBecause the flue gas in the firebox is a poor radiator, the equation must be corrected using an exchange factor which is dependent on the emissivity of the gas and the ratio of refractory area to cold plane area. Since the tubes themselves are not perfect absorbers, the curves are based on a tube-surface absorptivity of 0.9. This is a value considered typical for oxidized metal surfaces. The overall radiant exchange factor, F, can be taken from the curve below as presented by Mekler & Fairall in Petroleum Refiner, June 1952.
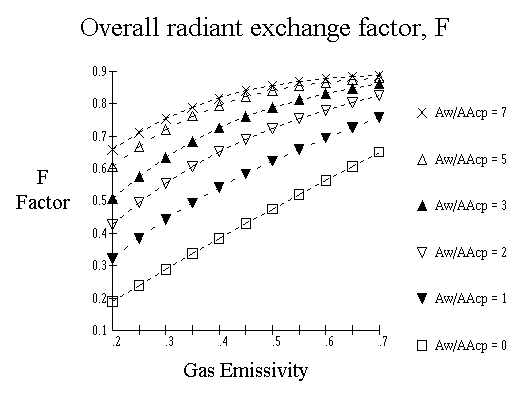
The equivalent cold plane area,aAcp, is the product of the effectiveness factor and the cold plane area as described above. The Aw can be described as follows,
| Aw = Ar - aAcp |
| and, |
| Aw = Effective refractory area, ft2 |
| Ar = Total refractory area, ft2 |
| aAcp = Equivalent cold plane area, ft2 |
The Ar factor is the inside area of the plenum in front of (or below, in some designs) the tubes. The openings where the flue gas enters are normally ignored, since the ducting connecting them perform the same reflective purpose.
Flue Gas Emissivity :The gas emissivity can be described by the curve presented by Lobo and Evans, at AICHE, 32nd Annual Meeting, November 1939. The tube wall temperature has only a minor effect. Therefore, the emissivity can be correlated as a function of PL product and the gas temperature, Tg. Variations in tube wall temperatures between 600 and 1200°F cause less than 1% deviation from these curves.
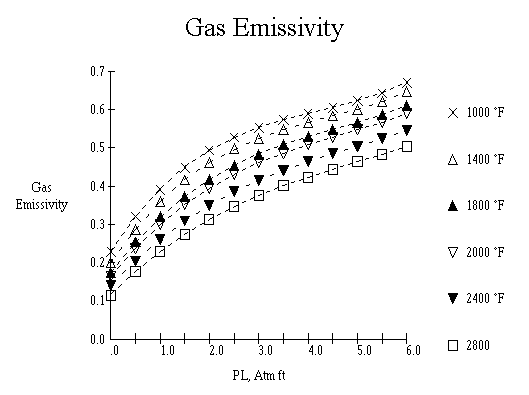
| PL = |
Product of the Partial Pressure of the carbon dioxide and water times the Beam Length, in atm-ft. |
| For Box Type Heaters | |
| Dimension Ratio | Mean Beam Length |
| 1-1-1 to 1-1-3 1-2-1 to 1-2-4 | 2/3(Furnace Volume)1/3 |
| 1-1-4 to 1-1-inf | 1 x Smallest Dimension |
| 1-2-5 to 1-2-inf | 1.3 x Smallest Dimension |
| 1-3-3 to 1-inf-inf | 1.8 x Smallest Dimension |
| With the box dimensions, length, width, and height being in any order | |
| For Vertical Cylindrical Heaters | |
| Length/Diameter < 2 | (((L/D)-1)*0.33 + 0.67)*D |
| Length/Diameter >= 2 | Diameter |
For most HRSG designs, the beam length can be taken as the width of the duct or superheter section.
Effective gas temperature in firebox, TgThis temperature is the calculated gas temperature entering the duct or plenum in front of the tube coil.
Average tube wall temperature, TwThe tube wall temperature calculation is discussed later in this section.
The radiant heat from this calculation will reduce the gas temperature used in the convection transfer calculation.
| To demonstrate this routine, we will assume that the gas temperature after firing is 1400 °F, and the tube wall temperature is 800 °F. We will assume that the gas prior to firing is the gas turbine exhaust we used in our example for calculating the heat balance. Gas Side : 800,000 lbs/hr of Gas Turbine Exhaust at 980 °F
|
 | ||||||||||||||||
To obtain the flue gas properties, we must do a combustion calculation. For this, we will assume fuel gas that is defaulted in the calculator below. The combustion process is covered in detail in Section 6, so for this exercise, we will just use a combustion calculator, such as the one below. Notice, that instead of firing with air as the source of oxygen, we use the exhaust gas for the oxygen source. For this case, we are not adding any additional air.
| Gas Properties After Firing: Volume % | |
| Nitrogen, N2 | 71.8121 |
| Oxygen, O2 | 10.1589 |
| Carbon Dioxide, CO2 | 4.7397 |
| Water, H2O | 12.4283 |
| Argon, Ar | 0.861 |
Now we can perform the calculations as follows,
From above, we determine a is equal to 1.
And,
Ar = 8 * 14 * 2 + 4 * 14 * 2 + 8 * 14.6 * 2 = 569.6 ft2
Acp = 23 * 16 = 368 ft2
Aw = 569.6 - 368 = 201.6 ft2
So, Aw/aAcp = 201.6 / 368 = 0.548
Partial Pressure of H2O and CO2 = 0.047397 + 0.124283 = 0.17168 atm
Beam length = width = 8 ft
PL = BL * PP = 8 * 0.17168 = 1.37344
For the emissivity and exchage factor, we can interpret the above curves or use the following JavaScripts.
Emissivity from curve = 0.342We now need to calculate the theoretical exit temp, then using the average of the 1400 and the exit temperature, recalculate the heat given up again, so it requires a few iterations to get a valid answer.
Enthalpy of flue gas after burner = 369.880 Btu/lbTo do this iteration in an efficient manner, we can set up a JavaScript to let our browser do this tedious work.
But before we do finalize our heat balance, we need to look at the distribution of this heat to the tubes. Since most of this radiant heat is absorbed by the first two rows of tubes, we will assume that only the first two rows are absorbing this heat. In actuality, some of the radiant heat would go to the third row, how much would depend on the tube diameter and spacing. But the amount to the third row is insignificant and can simply be added to the second row which will be more conservative. For the distribution to the first row of tubes, we can use the alpha, from the curves above, for direct to one row. We can use the following JavaScript to interpret the curve.
So, for our sample calculation, the radiant heat would be distributed, 70% to the first row and 30% to the second row.